...
Decibels
The decibel (dB) is used to measure sound level but it is also used widely in communications, electronics and signals. In communications, the decibel is a logarithm way of describing a ratio between two signal power, such as power, sound pressure, voltage, or current levels The decibel is a common measurement used in the field of electronics to determine loss or gain in a system.
Suppose we have 2 signals, signal 1 has a power of P1 watts, signal 2 has a power of P2 Watts, then the difference in decibels between 2 signals is defined to be:
10log(P2/P1)dB where the log is base 10
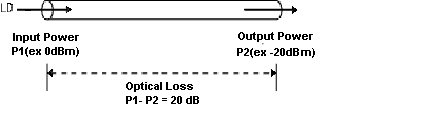
In order to measure optical loss, you can use two units, namely, dBm and dB. While dBm is the actual power level represented in milliwatts, dB (decibel) is the difference between the powers.
Figure 4 – How to Measure Optical Power
Figure 1: How to measure optical power [1]
Light loss, L(dB), is a commonly used specification for fiber optic attenuation. For example, to determine the light loss of an optical fiber in a cable, a light source is connected to one end of the fiber cable (input). The light output power of the source is known to be 0.1 mW. When an optical power meter is connected to the opposite end of the fiber optic cable under test (output), the meter measures 0.05 mW. Using the decibel power loss formula, the optical fiber loss can be calculated as follows:
Figure 2: How to measure fiber loss [2]
The light power loss of this optical fiber is 3 dB
The dB unit is a logarithmic ratio of input and output levels and is therefore not absolute (i.e., has no units). An absolute measure of power in decibels can be made in the dBm form. The dBm unit is a logarithmic ratio of the measured power to 1 mW of reference power
Reference
- Introduction to optical fibers, dB, Attenuation and measurement:
http://www.cisco.com/c/en/us/support/docs/optical/synchronous-digital-hierarchy-sdh/29000-db-29000.html - Optical Power loss measurement in db- how to measure it fast and correct
http://www.ad-net.com.tw/?id=474
...
Frequency
Attenuation always serves as a measurement parameter that leads to the formation of theories to explain physical or chemical phenomenon, which decreases the ultrasonic intensity. Attenuation is generally proportional to the square of sound frequency. Quoted values of attenuation are often given for a single frequency, or an attenuation value averaged over many frequencies may be given. The attenuation coefficient (α) can be used to determine total attenuation in dB in the medium using the following formula:
α: attenuation coefficient
The attenuation coefficients of common biological materials at a frequency of 1 MHz are listed below:
| Material | a (dB / (MHz ; cm)) |
|---|---|
| Air | 1.64 (20°C) |
| Blood | 0.2 |
| Bone, cortical | 6.9 |
| Bone, trabecular | 9.94 |
| Brain | 0.6 |
| Breast | 0.75 |
| Cardiac | 0.52 |
| Connective tissue | 1.57 |
| Dentin | 80 |
| Enamel | 120 |
| Fat | 0.48 |
| Liver | 0.5 |
| Marrow | 0.5 |
| Muscle | 1.09 |
| Tendon | 4.7 |
| Soft tissue (average) | 0.54 |
| Water | 0.0022 |
Figure 1. Diffuse reflection. Copied from [1]
- Culjat, Martin O.; Goldenberg, David; Tewari, Priyamvada; Singh, Rahul S. (2010). "A Review of Tissue Substitutes for Ultrasound Imaging". Ultrasound in Medicine & Biology 36 (6): 861–873.
- Tole, Nimrod M. (2005). Basic physics of ultrasonographic imaging.
Chapter 3: http://www.isradiology.org/isr/docs_books/basic/Chapter3.pdf - Michael L. Oelzea; William D. O’Brien, Jr. (2002). Frequency-dependent attenuation-compensation functions for ultrasonic signals backscattered from random media.
...