Authors: Tan Phat Chau, Minh Thai Nguyen, Nhat Minh Nguyen & Thai Binh Nguyen
Table of Contents
Optical amplifiers
Optical link has limit in range as there is always attenuation of propagating light in a normal fiber. One method to solve the problem is to detect the optical signal before the critical low value and convert it back to electrical domain and create new copy of optical signal. Another method is using optical amplifier. Without need of converting back optical signal to electrical domain, an amplifier can be used in different applications. It can be use as an inline amplifiers to compensate the attenuation of optical signals as well as pre-amplifiers in optical detectors to improve sensitivity of the receiver or as power boosters to raise output power of an optical transmitter.[1,149]
There are two categories of amplifiers: semiconductor optical amplifiers (SOAs) and fiber amplifiers. Optical gain in semiconductors is based on forward-biased junction. Fiber amplifier contains optical fiber which is doped with a rare earth element such as neodymium (Nd) and praseodymium (pr) etc… The existence of dopants creates new energy bands within the fiber.
Figure1: Band diagram of a doped fiber amplifier. Copied from Azadeh, M. (2009). Fiber optics engineering.[1,150]
Figure 1 illustrates the dopants ions interact with the pump signal with frequency fp and goes to higher energy state Ep . The ions have short lifetime ( Tp ) and quickly move to lower energy band, Et , in which they have longer lifetime ( Tl ). Because Tl >> Tp , population inversion is created. Inverted system interacts with main signal of frequency f , results in amplification of signal as stimulated emission happens.
The erbium doped fiber amplifier (EDFA) is the most popular type as El – Eo exists in the wavelength of 1550 nm. In consequence, EDFA can amplify signal in lowest range of attenuation of silica fibers, results in the popularity of using in long distance communication. Typical EDFA amplifiers can supply gain in 30nm band (1530-1560 nm) with gain of 20-30 dB.
Figure 2: Sample EDFA configuration. Copied from Azadeh, M. (2009). Fiber optics engineering.[1,151]
Figure 2 shows one example of co-directional pumping as the main and pump signals travel in same direction. EDFAs have very important role in long-range optical fiber communication, and subjected to high interest of researching for increase of bandwidth and performance.
Decibels
The decibel (dB) is used to measure sound level but it is also used widely in communications, electronics and signals. In communications, the decibel is a logarithm way of describing a ratio between two signal power, such as power, sound pressure, voltage, or current levels The decibel is a common measurement used in the field of electronics to determine loss or gain in a system.
Suppose we have 2 signals, signal 1 has a power of P1 watts, signal 2 has a power of P2 Watts, then the difference in decibels between 2 signals is defined to be:
10log(P2/P1)dB where the log is base 10
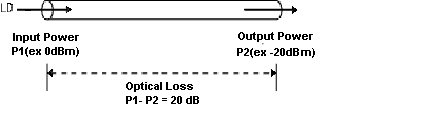
In order to measure optical loss, you can use two units, namely, dBm and dB. While dBm is the actual power level represented in milliwatts, dB (decibel) is the difference between the powers.
Figure 4 – How to Measure Optical Power
Figure 1: How to measure optical power [1]
Light loss, L(dB), is a commonly used specification for fiber optic attenuation. For example, to determine the light loss of an optical fiber in a cable, a light source is connected to one end of the fiber cable (input). The light output power of the source is known to be 0.1 mW. When an optical power meter is connected to the opposite end of the fiber optic cable under test (output), the meter measures 0.05 mW. Using the decibel power loss formula, the optical fiber loss can be calculated as follows:
Figure 2: How to measure fiber loss [2]
The light power loss of this optical fiber is 3 dB
The dB unit is a logarithmic ratio of input and output levels and is therefore not absolute (i.e., has no units). An absolute measure of power in decibels can be made in the dBm form. The dBm unit is a logarithmic ratio of the measured power to 1 mW of reference power
Reference
- Introduction to optical fibers, dB, Attenuation and measurement:
http://www.cisco.com/c/en/us/support/docs/optical/synchronous-digital-hierarchy-sdh/29000-db-29000.html - Optical Power loss measurement in db- how to measure it fast and correct
http://www.ad-net.com.tw/?id=474
Other Variable Dependencies
References
- Reflection and the Ray Model of Light - Lesson 1 - Reflection and its Importance
http://www.physicsclassroom.com/class/refln/Lesson-1/Specular-vs-Diffuse-Reflection - B.G. Potter. Module 3 - Attenuation in optical fibers
http://opti500.cian-erc.org/opti500/pdf/sm/Module3%20Optical%20Attenuation.pdf
Frequency
Attenuation always serves as a measurement parameter that leads to the formation of theories to explain physical or chemical phenomenon, which decreases the ultrasonic intensity. Attenuation is generally proportional to the square of sound frequency. Quoted values of attenuation are often given for a single frequency, or an attenuation value averaged over many frequencies may be given. The attenuation coefficient (α) can be used to determine total attenuation in dB in the medium using the following formula:
α: attenuation coefficient
The attenuation coefficients of common biological materials at a frequency of 1 MHz are listed below:
| Material | a (dB / (MHz ; cm)) |
|---|---|
| Air | 1.64 (20°C) |
| Blood | 0.2 |
| Bone, cortical | 6.9 |
| Bone, trabecular | 9.94 |
| Brain | 0.6 |
| Breast | 0.75 |
| Cardiac | 0.52 |
| Connective tissue | 1.57 |
| Dentin | 80 |
| Enamel | 120 |
| Fat | 0.48 |
| Liver | 0.5 |
| Marrow | 0.5 |
| Muscle | 1.09 |
| Tendon | 4.7 |
| Soft tissue (average) | 0.54 |
| Water | 0.0022 |
Figure 1. Diffuse reflection. Copied from [1]
References
- Culjat, Martin O.; Goldenberg, David; Tewari, Priyamvada; Singh, Rahul S. (2010). "A Review of Tissue Substitutes for Ultrasound Imaging". Ultrasound in Medicine & Biology 36 (6): 861–873.
- Tole, Nimrod M. (2005). Basic physics of ultrasonographic imaging.
Chapter 3: http://www.isradiology.org/isr/docs_books/basic/Chapter3.pdf - Michael L. Oelzea; William D. O’Brien, Jr. (2002). Frequency-dependent attenuation-compensation functions for ultrasonic signals backscattered from random media.
Transparency in optical fibers
Optical fibers have held a key role in making growth of world-wide communications and internet. The creation of very pure glass which is sufficiently transparent that makes possibility of long distance transmission of light through glass fibers. In 1960, working in research laboratory in California, Theodore Maiman produced the first operating laser which has very pure nature, well-defined color and is very bright. The special properties of laser create opportunities to expand the usefulness of optical communication links. In addition, the creation of a reliable, affordable channel for long distances data transmission is required to advance optical communication. In 1854, in London, John Tyndall shown that light can be guided along a stream of flowing water that proves light needs not to travel in straight lines.[1]
An optical waveguide must be made from a transparent material which can be plastics or glasses. Optical attenuation in plastics is much higher than the attenuation in glasses. Materials such as polystyrene or polymethacrylates (PMMA) are often used plastic fibers with losses in range of 100-1000 dB/km. However, plastic fibers are easy to manufacture so that is an economic solution for short-range communication. Nevertheless, glasses are excellent materials for optical waveguides as those have very low loss.[2,128]
Total internal reflection theory was applied in guiding light in optical fibers. When a light ray passes from a transparent medium to another, it bends at the boundary of two media. The bending phenomenon can be described by Snell’s law mathematically:
a first sense q 1 = n 2 sin q 2
Figure1: Refractive indices of media and Snell’s law. Copied from [1].
As figure 1 shows that is n2 is less than n1, there is restriction of the angles that light ray can go cross the border. Light goes from medium 1 to medium 2 with condition that f1 is greater than the critical angle so light cannot refract across the boundary (because f1 cannot greater than 90). The critical angle is defined by sine of n2/n1. A light ray goes to the boundary at an angle which is greater than the critical angle, it reflects and does not cross the border.[1]
Figure 2: Total internal reflection. Copied from [1].
Figure 2 shows typical structure of an optical fiber with the capability of guiding light ray inside by applying the total internal reflection between the core glass and the less dense glass surrounding.
In 1958, fiber imaging bundles were developed for medical imaging. In that bundle, a large number of optical fibers are bonded together. Optical image is relayed from one end of bundle and appears at the other end, where it can be seen. It was concluded that about 80 percents of the original light is transmitted to other end with a bundle 1m long. However with 100m long bundle, only a ten billionth part of the light reaches the far end. The attenuation of bundle was measured as 1000 dB per km, which can be considered useless for long distance light transmission.[1]
In 1966, Charles Kao and George Hockham pointed out that glass attenuation has reason in the impurity with appearance of metal ions, such as iron, copper, vanadium and chromium and a glass with attenuation of 20 dB/km can make 1% of input light reaches the other end of a 1 km-length fiber. In 1979 the attenuation of 0.2 dB/km was achieved in optical fiber.[1]